内蒙古包头市第二届互联网大会举办

Gerade quadratische Pyramide

Schiefe quadratische Pyramide

Unregelm??ige schiefe Pyramiden mit konvexem (links) bzw. konkavem Polygon

百度 各级党组织应在不同层次、不同领域的协商民主活动中充分发挥领导作用，对民主协商的议题、程序、方法、过程、结果等进行引导、组织，推动协商民主与国家治理有效衔接，进一步拓宽民主协商的渠道，加强协商民主的制度化、法治化、程序化建设。

In der Geometrie ist eine Pyramide ein geometrischer K?rper (genauer ein Polyeder), dessen Kanten aus den Kanten eines ebenen Polygons (der Grundfl?che) und den Verbindungsstrecken der Ecken des Polygons mit einem nicht in der Polygonebene gelegenen Punkt $S$ (der Spitze) bestehen. Im bekanntesten Fall ist das Polygon ein Quadrat und die Spitze $S$ ein Punkt senkrecht über dem Mittelpunkt des Quadrates. In diesem Fall entsteht eine gerade quadratische Pyramide. Liegt $S$ nicht über dem Mittelpunkt des Quadrats, liegt eine schiefe quadratische Pyramide vor.

Bezeichnungen:
Die Gesamtheit der Seitenfl?chen einer Pyramide (= Oberfl?che) besteht aus dem gegebenen Polygon, der Grundfl?che, und aus Dreiecken mit dem gemeinsamen Punkt $S$. Die Dreiecke bilden zusammen den Mantel der Pyramide. Die Kanten des Polygons hei?en Grundkanten und die Kanten durch $S$ Seitenkanten.

Ist das Polygon regelm??ig, d. h. sind die Kanten gleich lang und liegen die Ecken auf einem Kreis mit Mittelpunkt $C$, so hei?t die Pyramide regelm??ig. Ist zus?tzlich $C$ der Lotfu?punkt von $S$ auf die Kreisebene, so hei?t die Pyramide gerade. Die Dreiecke sind dann alle kongruent und gleichschenklig. Alle anderen Pyramiden hei?en schief.

Der Begriff gerade Pyramide wird nicht einheitlich verwendet. Die englische Wikipedia verlangt nur, dass der Lotfu?punkt der Spitze mit dem geometrischen Schwerpunkt zusammenf?llt.

Verbindung zu einem Kegel: Ersetzt man das Polygon durch eine Kurve, z. B. einen Kreis, und verbindet jeden Punkt der Kurve mit der Spitze, erh?lt man einen Kegel.

Eigenschaften

Allgemein

Hat das Polygon $n$ Ecken, den Fl?cheninhalt $G$ und ist die H?he der Pyramide $h$, so gilt:

1. Anzahl der Ecken: $n+1$
2. Anzahl der Fl?chen: $n+1$
3. Anzahl der Kanten: $2n$
4. Volumen: $V={\tfrac {1}{3}}Gh$
5. Der Schwerpunkt $C'$ der Pyramide teilt die Strecke zwischen dem Mittelpunkt der Grundfl?che $C$ und der Spitze $S$ im Verh?ltnis $1:3$.

Im Fall $n=3$ nennt man die Pyramide Tetraeder.

Gerade quadratische Pyramide

Gerade quadratische Pyramide: Bezeichnungen

Es sei $a$ die Quadratl?nge und $h$ die H?he der Pyramide.

Geometrische Eigenschaften

$n=4,\ G=a^{2}$

H?he der Dreiecke: $h'={\sqrt {h^{2}+{\frac {a^{2}}{4}}}}$

Dreiecksfl?che: ${\frac {a}{2}}{\sqrt {h^{2}+{\frac {a^{2}}{4}}}}$

L?nge der Kanten durch die Spitze: $l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}$

Volumen: $V={\frac {1}{3}}a^{2}h$

Oberfl?che: $O=a^{2}+a\cdot {\sqrt {4\cdot h^{2}+a^{2}}}$

H?he des Schwerpunkts $C'$ über dem Mittelpunkt der Grundfl?che $C$: $s={\frac {h}{4}}$

Weitere Eigenschaften enth?lt der Abschnitt Formeln für regelm??ige Pyramiden.

Johnson-K?rper

Links: Johnson-K?rper
Rechts: Pyramide mit maximalem Volumen bei vorgegebener Oberfl?che

Eine quadratische Pyramide, deren vier dreieckige Seitenfl?chen gleichseitig sind, ist der einfachste Johnson-K?rper, abgekürzt mit $J_{1}$. In diesem Fall gilt $h={\frac {a}{2}}\cdot {\sqrt {2}}$ und die Pyramide ist ein halbes regul?res Oktaeder. Verdoppelt man die H?he, erh?lt man die Pyramide mit maximalem Volumen bei vorgegebener Oberfl?che.

Maximales Volumen

Unter allen quadratischen Pyramiden mit vorgegebener Oberfl?che $O$ hat diejenige das gr??te Volumen, für die

$a={\frac {\sqrt {O}}{2}},\quad h={\sqrt {\frac {O}{2}}}\quad$ und damit $\quad h=a\cdot {\sqrt {2}}$

gilt. Ihr Volumen ist dann $V={\frac {1}{3}}\cdot a^{3}\cdot {\sqrt {2}}={\frac {O{\sqrt {O}}}{12{\sqrt {2}}}}$.

Zum Nachweis l?se man $\;O=a^{2}+a{\sqrt {4h^{2}+a^{2}}}\;$ nach $h^{2}$ auf, setze es in $U=9V^{2}=a^{4}h^{2}$ ein und bestimme das lokale Maximum von $U(a)$.

Formeln für regelm??ige Pyramiden

Tabelle

Die Tabelle enth?lt Formeln für geometrische Eigenschaften einer allgemeinen regelm??igen gerade Pyramide (2. Spalte). In der 3. und 4. Spalte speziell für die F?lle $n=4$ und $n=3$.

Regelm??ige gerade Pyramiden: Bezeichnungen für die Formeltabelle

Gr??en einer regelm??igen Pyramide mit der H?he h und einem regelm??igen n-Eck mit Seitenl?nge a als Grundfl?che
	Allgemeiner Fall	Quadratische Pyramide	Regelm??ige Dreieckspyramide
Volumen	$V={\frac {na^{2}h}{12}}\cot \left({\frac {\pi }{n}}\right)$	$V={\frac {a^{2}h}{3}}$	$V={\frac {a^{2}h}{12}}{\sqrt {3}}$
Oberfl?che	$O={\frac {na}{4}}\left(a\cot \left({\frac {\pi }{n}}\right)+{\sqrt {4h^{2}+a^{2}\cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)$	$O=a^{2}+a{\sqrt {4h^{2}+a^{2}}}$	$O={\frac {3a}{4}}\left({\frac {a}{3}}{\sqrt {3}}+{\sqrt {4h^{2}+{\frac {a^{2}}{3}}}}\right)$
Seitenkantenl?nge	$l=\left(h^{2}+{\frac {a^{2}}{4\sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}$	$l={\sqrt {h^{2}+{\frac {a^{2}}{2}}}}$	$l={\sqrt {h^{2}+{\frac {a^{2}}{3}}}}$
Umkugelradius	$r_{u}={\frac {h}{2}}+{\frac {a^{2}}{8h\sin ^{2}\left({\frac {\pi }{n}}\right)}}$	$r_{u}={\frac {h}{2}}+{\frac {a^{2}}{4h}}$	$r_{u}={\frac {h}{2}}+{\frac {a^{2}}{6h}}$
Inkugelradius	$r_{i}={\frac {ah}{a+{\sqrt {4h^{2}\tan ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}}}}$	$r_{i}={\frac {ah}{a+{\sqrt {4h^{2}+a^{2}}}}}$	$r_{i}={\frac {ah}{a+{\sqrt {12h^{2}+a^{2}}}}}$
Basiswinkel der gleichschenkligen Dreiecke $\alpha _{2}=\alpha _{1}$	$\alpha _{1}=\arctan \left({\frac {1}{a}}{\sqrt {4h^{2}+a^{2}\cot ^{2}\left({\frac {\pi }{n}}\right)}}\right)$	$\alpha _{1}=\arctan \left({\frac {1}{a}}{\sqrt {4h^{2}+a^{2}}}\right)$	$\alpha _{1}=\arctan \left({\frac {1}{a}}{\sqrt {4h^{2}+{\frac {a^{2}}{3}}}}\right)$
Winkel an der Spitze der gleichschenkligen Dreiecke	$\alpha _{3}=2\arctan \left({\frac {a}{\sqrt {4h^{2}+a^{2}\cot ^{2}\left({\frac {\pi }{n}}\right)}}}\right)$	$\alpha _{3}=2\arctan \left({\frac {a}{\sqrt {4h^{2}+a^{2}}}}\right)$	$\alpha _{3}=2\arctan \left({\frac {a}{\sqrt {4h^{2}+{\frac {a^{2}}{3}}}}}\right)$
Winkel zwischen Grundfl?che und gleichschenkligen Dreiecken	$\beta _{1}=\arctan \left({\frac {2h\tan \left({\frac {\pi }{n}}\right)}{a}}\right)$	$\beta _{1}=\arctan \left({\frac {2h}{a}}\right)$	$\beta _{1}=\arctan \left({\frac {2{\sqrt {3}}h}{a}}\right)$
Winkel zwischen den gleichschenkligen Dreiecken	$\beta _{2}=2\arctan \left({\frac {1}{2h}}\left({\frac {4h^{2}\sin ^{2}\left({\frac {\pi }{n}}\right)+a^{2}}{\tan ^{2}\left({\frac {\pi }{n}}\right)-\sin ^{2}\left({\frac {\pi }{n}}\right)}}\right)^{\frac {1}{2}}\right)$	$\beta _{2}=2\arctan \left({\frac {1}{2h}}{\sqrt {4h^{2}+2a^{2}}}\right)$	$\beta _{2}=2\arctan \left({\frac {1}{3h}}{\sqrt {3h^{2}+a^{2}}}\right)$
Winkel zwischen Seitenkante und Grundfl?che	$\gamma =\arctan \left({\frac {2h\sin \left({\frac {\pi }{n}}\right)}{a}}\right)$	$\gamma =\arctan \left({\frac {2h}{{\sqrt {2}}a}}\right)$	$\gamma =\arctan \left({\frac {{\sqrt {3}}h}{a}}\right)$
Raumwinkel an der Grundfl?che	$\Omega _{1}=4\arctan \left({\sqrt {\tan \left({\frac {2\beta _{1}+\beta _{2}}{4}}\right)\tan \left({\frac {2\beta _{1}-\beta _{2}}{4}}\right)\tan ^{2}\left({\frac {\beta _{2}}{4}}\right)}}\right)$
Raumwinkel in der Spitze	$\Omega _{2}=2\pi -2n\arcsin \left(\cos \left({\frac {\pi }{n}}\right){\sqrt {\tan ^{2}\left({\frac {\pi }{n}}\right)-\tan ^{2}\left({\frac {\alpha _{3}}{2}}\right)}}\right)$

Spezialf?lle

Pyramide als Teil eines Ikosaeders

Für bestimmte Werte von $n$ und $h$ ergeben sich Zusammenh?nge mit platonischen K?rpern:

• Für $n=3$ und $h={\frac {a}{3}}{\sqrt {6}}$ ergibt sich das regelm??ige Tetraeder.
• Für $n=4$ und $h={\frac {a}{2}}{\sqrt {2}}$ ergibt sich eine quadratische Pyramide, die ein halbes regul?res Oktaeder ist.
• Für $n=5$ und $h={\frac {a}{10}}{\sqrt {50-10{\sqrt {5}}}}$ ergibt sich eine regelm??ige fünfseitige Pyramide, die ein Teil des Ikosaeders ist.

Maximales Volumen im Fall n

Pyramiden mit maximalem Volumen bei vorgegebener Oberfl?che $O$,
rot: Kegel mit derselben Eigenschaft und derselben Oberfl?che
$V_{\text{Pyram}}/V_{\text{Kegel}}$:
$n=3:\;0{,}78\quad n=4:\;0{,}89$
$n=6:\;0{,}95\quad n=10:\;0{,}98$

Mit überlegungen wie für eine gerade quadratische Pyramide (siehe oben) zeigt man:

Unter allen geraden regul?ren n-seitigen Pyramiden mit vorgegebener Oberfl?che $O$ hat diejenige das gr??te Volumen, für die

$a={\sqrt {\frac {O}{n\cot {\frac {\pi }{n}}}}},$

$h={\sqrt {2\;O}}\;{\sqrt {\frac {\cot {\frac {\pi }{n}}}{n}}}={\sqrt {\tfrac {2\;O}{\pi }}}\cdot {\sqrt {{\tfrac {\pi }{n}}\cot {\tfrac {\pi }{n}}}}$

und damit $\ h=a{\sqrt {2}}\cot {\tfrac {\pi }{n}}\$ gilt.

Der Umkreisradius des Basispolygons ist

$\ r_{u}={\frac {a}{2\sin {\tfrac {\pi }{n}}}}={\sqrt {\tfrac {O}{4\pi }}}\cdot {\sqrt {\frac {\tfrac {2\pi }{n}}{\sin {\frac {2\pi }{n}}}}}\$.

Das maximale Volumen ist $V={\tfrac {O}{12}}{\sqrt {\tfrac {2\;O}{\pi }}}\cdot {\sqrt {{\tfrac {\pi }{n}}\cot {\tfrac {\pi }{n}}}}\$.

Für $n$ gegen unendlich geht $a$ monoton fallend gegen $0$ und $h$ monoton steigend gegen $h_{k}={\sqrt {\tfrac {2\;O}{\pi }}}$. Letzteres ist die H?he eines Kegels mit maximalem Volumen bei vorgegebener Oberfl?che $O$. (Bei der Grenzwertbildung wird $\lim _{x\to 0}{\tfrac {\sin x}{x}}=1$ verwendet.)
Der Radius des Basiskreises des optimalen Kegels ist $\ r_{k}={\sqrt {\tfrac {O}{4\pi }}}$,
seine H?he $\ h_{k}=2{\sqrt {2}}\;r_{k}={\sqrt {\tfrac {2\;O}{\pi }}}\$ und
sein Volumen $\ V_{k}={\tfrac {O}{12}}{\sqrt {\tfrac {2\;O}{\pi }}}\$.

Für das Verh?ltnis der Volumina gilt:

${\frac {V_{\text{Pyram}}}{V_{\text{Kegel}}}}={\sqrt {{\frac {\pi }{n}}\cot {\frac {\pi }{n}}}}$,

das für $n\to \infty$ gegen 1 strebt.

Zusammenhang mit dem Kreiskegel

Pyramide zur Approximation eines Kegels

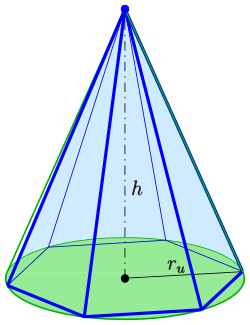
Regelm??ige Pyramiden, die ein regelm??iges Vieleck als Grundfl?che haben, k?nnen verwendet werden, um einen Kreiskegel zu approximieren, der nach Definition einen Kreis als Grundfl?che hat.

Wenn das regelm??ige Vieleck $n$ Ecken hat, also ein $n$-Eck ist, kann formal der Grenzwert für unendlich gro?es $n$ gebildet werden. Der Kreiskegel kann sozusagen als regelm??ige Pyramide aufgefasst werden, wobei die Grundfl?che unendlich viele Ecken und die Seitenl?nge des $n$-Ecks den Grenzwert 0 hat.

Im Folgenden soll auf diese Weise das Volumen des Kreiskegels hergeleitet werden.

Mithilfe der Formel für den Fl?cheninhalt eines regelm??igen $n$-Ecks (siehe Regelm??iges Polygon – Umfang und Fl?cheninhalt) ergibt sich für das Volumen $V$ der regelm??igen Pyramide, wenn der Umkreisradius $r_{u}$ des $n$-Ecks bekannt ist:

$V={\frac {Gh}{3}}=n{\frac {r_{u}^{2}}{2}}\sin \left({\frac {2\pi }{n}}\right){\frac {h}{3}}={\frac {nr_{u}^{2}h}{6}}\sin \left({\frac {2\pi }{n}}\right)$

Um das Volumen des Kreiskegels zu bestimmen, kann der Grenzwert für $n$ gegen unendlich gebildet werden. Dieser Grenzwert ergibt sich mit Hilfe der Formel $\lim _{x\to 0}{\tfrac {\sin x}{x}}=1$:

$V_{\text{Kreiskegel}}=\lim _{n\to \infty }{\frac {Gh}{3}}=\lim _{n\to \infty }{\frac {n\,r_{u}^{2}\,h}{6}}\sin \left({\frac {2\pi }{n}}\right)$

$\qquad \qquad ={\frac {r_{u}^{2}\,h}{6}}2\pi \cdot \lim _{n\to \infty }{\frac {\sin \left({\frac {2\pi }{n}}\right)}{\frac {2\pi }{n}}}={\frac {r_{u}^{2}\,h}{6}}2\pi \cdot 1={\frac {1}{3}}\pi r_{u}^{2}\cdot h$

Herleitung der Volumenformel für die allgemeine Pyramide

Für die Herleitung des Volumens einer allgemeinen Pyramide gibt es mehrere Wege:

Berechnung mit Hilfe des Spatprodukts

Eine von den Vektoren ${\vec {a}},{\vec {b}},{\vec {c}}$ aufgespannte dreiseitige Pyramide hat das Volumen

$V={\frac {1}{6}}\cdot \left|\left({\vec {a}}\times {\vec {b}}\right)\cdot {\vec {c}}\right|.$

Siehe auch: Spatprodukt

Elementargeometrische Begründung

Die erw?hnte Volumenformel l?sst sich elementargeometrisch in zwei Schritten begründen:

1. Ein Würfel kann in drei gleiche Pyramiden mit quadratischer Grundfl?che zerlegt werden, deren Spitzen in einer Ecke des Würfels zusammenfallen. Die drei Grundfl?chen sind die drei Seitenfl?chen des Würfels, die diese gemeinsame Spitze nicht enthalten.
2. Zwei Pyramiden mit gleicher Grundfl?che und gleicher H?he stimmen im Volumen überein.

Zum Beweis dieser Aussage kann man das Prinzip von Cavalieri und die Gesetze der zentrischen Streckung heranziehen.

Für Pyramiden gilt demzufolge die Volumenformel

$V={\frac {1}{3}}\cdot G\cdot h.$

Begründung mit Hilfe der Integralrechnung

Der Rauminhalt einer Pyramide mit der Grundfl?che $G$ und der H?he $h$ kann berechnet werden, wenn man sich die Pyramide aus dünnen (infinitesimalen) Schichten der Dicke $\mathrm {d} y$ parallel zur Grundfl?che aufgebaut vorstellt. Eine $y$-Achse lege man nun durch die Spitze der Pyramide, sodass die H?he $h$ mit der $y$-Achse zusammenf?llt. Bezeichnet man die Fl?che der Schicht im Abstand $y$ von der Spitze mit $A(y)$, so kann man aus den Gesetzen der zentrischen Streckung eine Formel für $A(y)$ herleiten:

$A(y):G=y^{2}:h^{2}$

$A(y)={\frac {G}{h^{2}}}y^{2}$

Daraus ergibt sich das Volumen der Pyramide durch Integration von $y=0$ bis $y=h$ nach dem Prinzip von Cavalieri:

$V=\int _{0}^{h}A(y)\,\mathrm {d} y=\int _{0}^{h}{\frac {G}{h^{2}}}y^{2}\,\mathrm {d} y={\frac {G}{h^{2}}}\int _{0}^{h}y^{2}\,\mathrm {d} y={\frac {G}{h^{2}}}\cdot {\frac {1}{3}}\left[y^{3}\right]_{0}^{h}={\frac {G}{h^{2}}}\cdot {\frac {1}{3}}\left[h^{3}-0\right]={\frac {1}{3}}G\cdot h$

Vermessung eines Pyramidenbauwerks

Betrachtung aus der Entfernung und Sehwinkelbestimmung in vereinfachter Form

Bei einer gro?en Pyramide lassen sich die Kantenl?ngen der Basis direkt gut vermessen, jedoch nicht die H?he, die nicht direkt zug?nglich ist. Im Folgenden sollen die grunds?tzlichen Schwierigkeiten dargelegt werden, die nicht so sehr mit der Methodik des Messverfahrens selbst zusammenh?ngen. Ein einfaches geometrisches Verfahren zur H?henbestimmung gr??erer Objekte ist die Betrachtung aus der Entfernung und die Bestimmung des Sehwinkels (in vereinfachter Form durch die nebenstehende Grafik aufgezeigt).

Im Abstand $s$ von der unteren Pyramidenkante wird die Spitze der Pyramide unter dem gemessenen Winkel $\alpha$ angepeilt. Der Abstand des Beobachtungspunktes von der Pyramidenspitze in horizontaler Linie ist somit der um die halbe Grundseite vermehrte Abstand von der Pyramidenkante $a/2+s.$ Die H?he $h$ ergibt sich aus der Formel in der Grafik. Damit w?re die Bestimmung der H?he kein gro?es Problem. Es gibt jedoch folgende Schwierigkeiten:

• Die Spitze der Pyramide liegt nicht unbedingt exakt über dem Mittelpunkt der Grundfl?che.
• Die L?nge der Basiskante der Pyramide ist nicht sauber bestimmbar (abgebrochene Steine, Erosion).
• Die Spitze ist nicht mehr vorhanden (abgetragen).
• Der Neigungswinkel der Pyramide ist schwer bestimmbar (Abtragung, Erosion).

Das entspricht bei den bekannten gro?en Pyramiden weitgehend der Realit?t. Es muss definiert werden, von welchem Bodenniveau aus die H?he der Pyramide gelten soll, also wo ihre Basis angenommen wird; von dieser aus muss die H?henabweichung des Beobachtungspunktes, an dem $\alpha$ gemessen wird, genau berücksichtigt werden. Die Winkelmessung selbst kann in der Regel sehr pr?zise ausgeführt werden. Angenommen, die Basisl?nge $a$ der Pyramide lie?e sich nicht genauer als auf 30 cm und damit die Entfernung $a/2+s$ zum Messpunkt nicht genauer als auf 15 cm bestimmen. Dadurch würde bei einem Sehwinkel $\alpha$ von angenommenen 35° die H?he um den Betrag von etwa 10 cm ungenau sein. Au?erdem soll noch der Neigungswinkel $\beta$ der Seitenfl?che bestimmt werden. Eine hypothetische gro?e Pyramide der Basisl?nge von 200 m und einer H?he von 140 m h?tte bei einer Ungenauigkeit der H?henangabe von 10 cm eine Ungenauigkeit der Neigungswinkelangabe von etwa einer Bogenminute (54°27′44″ bei $h=140{,}0\,\mathrm {m}$ gegenüber 54°26′34″ mit $h=139{,}9\,\mathrm {m}$). Das gilt nun für Pyramiden, deren Spitze noch vorhanden ist. Die Realit?t sieht aber anders aus. Die H?henbestimmung gibt also nicht die ursprüngliche H?he wieder, sondern die H?he der abgetragenen Pyramide.

Problem bei Extrapolation

Die Spitze muss also extrapoliert werden. Das nebenstehende Bild zeigt schematisch das Problem. Sowohl die Seitenfl?chen als auch die Spitze sind durch Abriss und Verwitterung deutlich abgetragen:

Die H?he $h$ w?re daher gem?? der Formel aus der direkten Bestimmung des Neigungswinkels $\beta$ zug?nglich. Wie ersichtlich, ist die Bestimmung mit gro?en Fehlern behaftet. Eine Ausnahme bildet die Chephren-Pyramide, weil diese im oberen Teil noch die originalen Decksteine hat. Der Winkel $\beta$ ist dadurch genauer bestimmbar als bei den anderen Pyramiden. Das erkl?rt die gute übereinstimmung verschiedener Autoren hinsichtlich des Neigungswinkels.

Damit wird klar, dass bei realen Pyramiden weder die H?he auf den Zentimeter noch der Neigungswinkel auf die Bogensekunde exakt angegeben werden kann.

Verwandte Begriffe

Verwandte Formen in der Geometrie sind der Pyramidenstumpf (eine parallel zur Grundfl?che ?abgeschnittene“ Pyramide) und die Doppelpyramide (ein Polyeder aus zwei spiegelsymmetrischen Pyramiden mit derselben Grundfl?che).

Eine Hyperpyramide ist eine Verallgemeinerung auf $n$ Dimensionen. Die in diesem Artikel beschriebene Pyramide ist eine dreidimensionale Hyperpyramide. Eine zweidimensionale Hyperpyramide w?re ein Dreieck, eine vierdimensionale ein Pentachoron.

Mit der Pyramide in der Architektur befasst sich der Artikel Pyramide (Bauwerk).

Weblinks

Commons: Pyramids (geometry) – Sammlung von Bildern, Videos und Audiodateien

• Eric W. Weisstein: Pyramid. In: MathWorld (englisch).